In the concluding few weblog posts of this series, nosotros discussed simple linear regression model. We discussed multivariate regression model and methods for selecting the correct model.
Fernando has at i time created a ameliorate model.
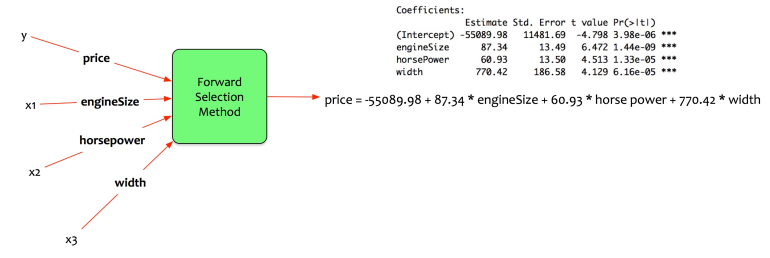
price = -55089.98 + 87.34 engineSize + 60.93 horse ability + 770.42 width
Fernando contemplates the following:
- How tin I guess the toll changes using a mutual unit of measurement of comparison?
- How elastic is the toll alongside abide by to engine size, Equus caballus power, too width?
In this article volition address that question. This article volition elaborate about Log-Log regression models.
The Concept:
To explicate the concept of the log-log regression model, nosotros require to select 2 steps back. First allow us empathize the concept of derivatives, logarithms, exponential. Then nosotros require empathize the concept of elasticity.
Derivatives:
Let us move dorsum to high schoolhouse math. Meet derivatives. One of most fascinating concepts taught inward high schoolhouse math too physics.
Derivate is a way to correspond change — the amount yesteryear which a business office is changing at i given point.
Influenza A virus subtype H5N1 variable y is a business office of x. Define y as:
y = f(x)
We apply derivative on y alongside abide by to x too correspond it every bit follows:
dy/dx = df(x)/dx = f’(x)
This agency the following:
- The modify inward y alongside abide by to modify inward x i.e. How much volition y modify if x changes?
Isn’t it that Fernando wants? He wants to know the modify inward toll (y) alongside abide by to changes inward other variables (cityMpg too highwayMpg).
Recall that the full general shape of a multivariate regression model is the following:
y = β0 + β1.x1 + β2.x2 + …+ βn.xn + 𝛆
Let us tell that Fernando builds the next model:
price = β0 + β1 . engine size i.e. expressing toll every bit a business office of engine size.
Fernando takes the derivative of toll alongside abide by to engine size. Shouldn’t he live able to limited the modify inward toll alongside abide by to changes inward engine size?
Alas, it is non that simple. The linear regression model assumes a linear relationship. The Linear human relationship is defined as:
y = mx + c
If the derivative of y over x is computed, it gives the following:
dy/dx = m . dx/dx + dc/dx
- The modify of something alongside abide by to itself is ever 1 i.e. dx/dx = 1
- The modify of a constant alongside abide by to anything is ever 0. That is why it is a constant. It won’t change. i.e. dc/dx = 0
The equation at i time becomes:
dy/dx = m
Applying derivate to toll on engine size volition yield null but the coefficient of engine size.
There has to live a way to transform it. Here come upwards 2 to a greater extent than mathematical characters. Meet exponential too logarithms.
Exponentials:
Now allow us await at exponential. This graphic symbol is i time to a greater extent than a mutual graphic symbol inward high schoolhouse math. An exponential is a business office that has 2 operators. Influenza A virus subtype H5N1 base of operations (b) too an exponent (n). It is defined as b^n. it takes the form:
f(x) = b^x
The base of operations tin live whatever positive number. Again Euler’s issue (e) is a mutual base of operations used inward statistics.
Geometrically, an exponential human relationship has next structure:
- An increment inward x doesn’t yield a corresponding increment inward y. Until a threshold is reached.
- After the threshold, the value of y shoots upwards chop-chop for a small-scale increment inward x.
Logarithms:
The logarithm is an interesting character. Let us exclusively empathize its personality applicable for regression models. The key holding of a logarithm is its base. The typical base of operations of the logarithm is 2, 10 or e.
Let us select an example:
- How many 2s practise nosotros multiply to acquire 8? 2 x 2 x 2 = 8 i.e. 3
- This tin every bit good live expressed as: log2(8) = 3
The logarithm of 8 alongside base of operations 2 is 3
There is some other mutual base of operations for logarithms. It is called every bit “Euler’s issue (e).” Its approximate value is 2.71828. It is widely used inward statistics. The logarithm alongside base of operations e is called as Natural Logarithm.
It every bit good has interesting transformative capabilities. It transforms an exponential relation into a linear relation. Let us await at an example:
The diagram below, shows an exponential human relationship betwixt y too x:
If logarithms are applied to both x too y, the human relationship betwixt log(x) too log(y) is linear. It looks something similar this:
Elasticity:
Elasticity is the mensuration of how responsive an economical variable is to a modify inward another.
Say that nosotros cause got a function: Q = f(P) hence the elasticity of Q is defined as:
eastward = P/Q x dQ/dP
- dq/dP is the average modify of Q wrt modify inward P.
Bringing it all together:
Now allow us convey these 3 mathematical characters together. Derivatives, Logarithms too Exponential. Their rules of appointment are every bit follows:
- Logarithm of e is 1 i.e. log(e) = 1
- The logarithm of an exponential is exponent multiplied yesteryear the base.
- Derivative of log(x) is : 1/x
Let us select an example. Imagine a business office y expressed every bit follows:
- y = b^x.
- => log(y) = x log (b)
So does it hateful for linear regression models? Can nosotros practise mathematical juggling to brand usage of derivatives, logarithms, too exponents? Can nosotros rewrite the linear model equation to detect the charge per unit of measurement of modify of y wrt modify inward x?
First, allow us define human relationship betwixt y too x every bit an exponential relationship
- y = α x^β
- Let us origin limited this every bit a business office of log-log: log(y) = log(α) + β.log(x)
- Doesn’t equation #1 await similar to regression model: Y= β0 + β1 . x1 ? where β0 = log(α); β1 = β. This equation tin live at i time rewritten as: log(y) = β0 + β1. log(x1)
- But how does it correspond elasticity? Let us select derivative of log(y) wrt x, nosotros acquire the following:
- d. log(y)/ dx = β1. log(x1)/dx.
- => 1/y . dy/dx = β1 . 1/x => β1 = x/y . dy/dx.
- The equation of β1 is the elasticity.
Model Building:
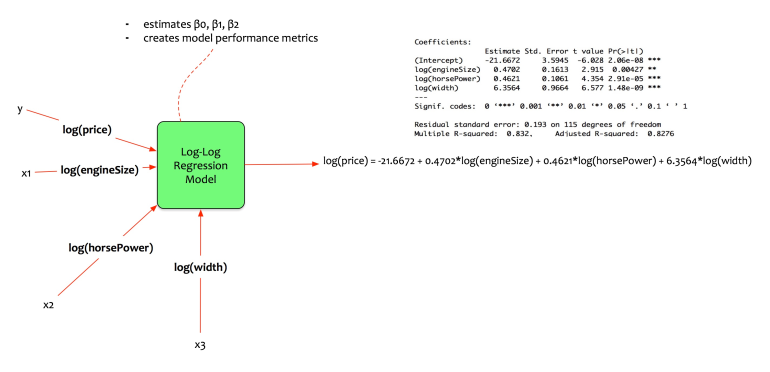
Now that nosotros empathize the concept, allow us run into how Fernando prepare a model. He builds the next model:
log(price) = β0 + β1. log(engine size) + β2. log(horse power) + β3. log(width)
He wants to guess the modify inward auto toll every bit a business office of the modify inward engine size, Equus caballus power, too width.
Fernando trains the model inward his statistical packet too gets the next coefficients.
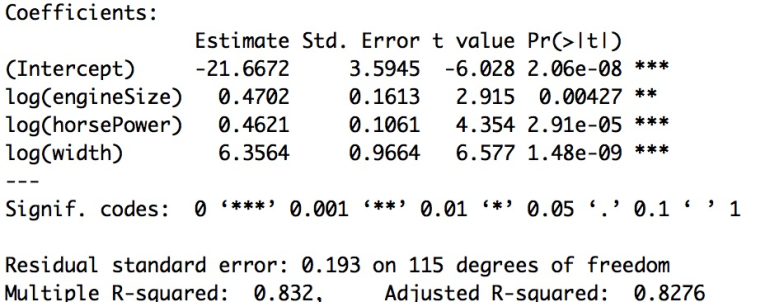
The equation of the model is:
log(price) = -21.6672 + 0.4702.log(engineSize) + 0.4621.log(horsePower) + 6.3564 .log(width)
Following is the interpretation of the model:
- All coefficients are significant.
- Adjusted r-squared is 0.8276 => the model explains 82.76% of variation inward data.
- If the engine size increases yesteryear 4.7% then the toll of the car increases yesteryear 10%.
- If the Equus caballus power increases yesteryear 4.62% then the toll of the car increases yesteryear 10%.
- If the width of the car increases yesteryear 6% then the toll of the car increases yesteryear 1 %.
Model Evaluation:
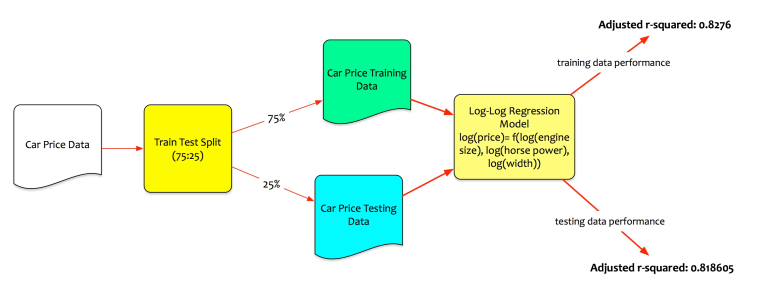
Fernando has at i time built the log-log regression model. He evaluates the performance of the model on both grooming too essay data.
Recall, that he had split the information into the grooming too the testing set. The grooming information is used to practise the model. The testing information is the unseen data. Performance on testing information is the existent test.
On the grooming data, the model performs quite well. The adjusted R-squared is 0.8276 => the model tin explicate 82.76% variation on grooming data. For the model to live acceptable, it every bit good needs to perform good on testing data.
Fernando tests the model performance on essay information set. The model computes the adjusted r-squared every bit 0.8186on testing data. This is good. It agency that model tin explicate 81.86% of variation fifty-fifty on unseen data.
Note that the model estimates the log(price) too non the toll of the car. To convert the estimated log(price) into the price, at that spot needs to live a transformation.
The transformation is treating the log(price) every bit an exponent to the base of operations e.
e^log(price)= price
Conclusion:
The concluding few posts cause got been quite a journey. Statistical learning laid the foundations. Hypothesis testing discussed the concept of NULL too alternate hypothesis. Simple linear regression models made regression simple. We hence progressed into the globe of multivariate regression models. Then discussed model alternative methods. In this post, nosotros discussed the log-log regression models.
So far the regression models built had exclusively numeric independent variables. The side yesteryear side postal service nosotros volition bargain alongside concepts of interactions too qualitative variables.
Originally published at datascientia.blog on August 14, 2017.
Sumber http://engdashboard.blogspot.com/